Prob & Stat 101

[krusader74]

Prob & Stat 101

Questions about probability theory appear from time to time on these boards, especially in regard to dice rolls. I wanted to create a "Prob & Stat 101" thread where people could

• Pose new probability and statistics questions
• Index past threads on prob & stat topics
• Discover free resources related to prob & stat such as dice rollers, textbooks, lectures, and software
• Share insights and interesting facts they've discovered

[krusader74]

An index of prob & stat related discussions

5e: 2
abilities: 1
approximation: 15
backgammon: 5
binomial distribution: 11, 16
calculators: 13
chain rule: 7
chainmail: 3
chi square test: 5, 6
complement rule: 7
convolutions: 10
cycle notation: 1
d10: 6
d20: 2, 6, 12
d6: 9, 10, 11
dF: 8
dice: 1, 2, 6, 8, 9, 10, 11, 12, 13, 14, 15
dice rollers: 14
enumeration: 10
fudge dice: 8
gems: 4
generating functions: 10
knights and magick: 10
knucklebones: 14
loaded dice: 5, 6
maximum: 2, 9, 12
median: 12
melee: 7, 17
minimum: 2, 9, 12
multiplication rule: 7
order statistics: 2, 9, 12
permutations: 1
polynomials: 10
product rule: 7
re-rolls: 1
saving throws: 15
simulation: 10, 17
software: 3, 4, 5, 13, 16, 17
statistical hypothesis test: 5, 6
subtraction rule: 7
tali: 14
u-shaped probability distributions: 1
z10: 10
zero-bias notation: 10

---

1: 3d6, re-roll 1's
Keywords: dice, re-rolls, u-shaped probability distributions, permutations, cycle notation, abilities

2: Advantatge/Disadvantage mechanic
Description: Calculate probabilities and statistics for 5E's advantage (and disadvantage) mechanic, i.e., max (and min) of two d20s.
Keywords: dice, order statistics, d20, minimum, maximum, 5e

3: Alternative Post Melee Morale
Description: Compute Chainmail post melee morale.
Keywords: software, chainmail

4: Analysis of OD&D treasure types
Description: Find the probabilities and statistics of 3LBB treasure types.
Keywords: software, gems

5: Backgammon/Chess/Cribbage
Description: Using the Chi Square test to check if dice are fair or loaded.
Keywords: loaded dice, chi square test, statistical hypothesis test, software, backgammon

6: Dice question. Percentile?
Description: Using two d10 as one d20. A post also mentions the use of the Chi Square test to check if dice are fair or loaded.
Keywords: dice, d10, d20, loaded dice, chi square test, statistical hypothesis test

7: From Man-To-Man Melee tbl. to Weapon Factors vs. unarmored
Description: Equi-probability of weapons to kill someone without armor in Chainmail.
Keywords: complement rule, subtraction rule, chain rule, multiplication rule, product rule, melee

8: Fudge dice
Description: Fudge dice look like six-sided dice, but they are labelled -1, 0, and 1 twice. The notation is dF for rolling one fudge die, 4dF for rolling four fudge dice and summing. A roll of 4dF produces numbers in the range -4 to 4. What is their distribution?
Keywords: dice, dF, fudge dice

9: Fuzzy on the statistics...
Description: Probabilities and statistics for min {d6, d6} and max {d6, d6}. A very detailed discussion of order statistics towards the end of the thread.
Keywords: dice, order statistics, d6, minimum, maximum

10: The math behind Knights and Magick
Description: Probabilities for z10 + d6.
Keywords: dice, zero-bias notation, convolutions, generating functions, polynomials, enumeration, simulation, d6, z10, knights and magick

11: Need Help With Probabilities-I'm math challenged!
Description: [T]he probability for rolling a certain face value on a d6 a certain number of times or greater.
Keywords: dice, binomial distribution, d6

12: Need some mathematical help
Description: Roll three d20. Find the distribution of the maximum, median, and minimum.
Keywords: dice, order statistics, d20, maximum, median, minimum

13: Number Appearing?
Description: 30-300 is what distribution? How to calculate? What's the mean and standard deviation?
Keywords: dice, software, calculators

14: Palamedes, knucklebones and virtual dice rollers
Description: Introduces several topics--

• Palamedes, the mythical inventor of numbers, money, dice and gambling.
• Knucklebones, the mythical first dice game.
• Tali, dice made from animal bones with non-equiprobable outcomes.
• Palamedes--an online dice roller, probability calculator and Bayesian belief net, authored by yours truly.

Keywords: dice, knucklebones, tali, dice rollers

15: Saving Throw Dice
Description: Convert saving throws from a d20 roll to a 3d6 roll or a d% roll.
Keywords: dice, approximation, saving throws

16: Solo play
Description: Use the probabilities calculated in A Veteran's Odds + the binomial distribution to compute the outcome of a fight during solo play.
Keywords: software, binomial distribution

17: A Veteran's Odds
Description: Level X fighter vs monster Y. What are the chances (mean and std. dev.) of a win, lose or draw?
Keywords: simulation, software, melee

[krusader74]

Free prob & stat resources

Textbooks & papers

A Collection of Dice Problems with solutions and useful appendices (a work continually in progress) version September 3, 2015 by Matthew M. Conroy. 83 pages. PDF.

Introduction to Probability (Version 2, 2008) by Charles M. Grinstead and J. Laurie Snell. 520 pages. PDF.

Basic Probability Theory (1970) by Robert B. Ash. 350 pages. Tragically, Professor Ash was struck by a car and died this April. He put many fine math books online including this one on probability theory available as individual chapters or as one big PDF (78MB).

Probability Theory--The Logic of Science (1996) by Edwin Thompson Jaynes. As HTML or the first 3 chapters as a 95-page PDF.

Introduction to Probability and Statistics Using R (2010) by G. Jay Kerns. 412 pages. PDF.

Software

Wolfram|Alpha is a free online computational knowledge engine (or answer engine) with free-form natural language input. See the Statistics & Data Analysis examples.

R is a freely available language and environment for statistical computing and graphics. Read the tutorial on probability distributions.

GNU PSPP is a program for statistical analysis of sampled data. It is a free open-source replacement for the proprietary program SPSS.

Maxima is a free cross-platform computer algebra system with support for probability distributions. See the online documentation on supported distributions.

SciPy is a Python-based ecosystem of open-source software for mathematics, science, and engineering. The scipy.stats module provides excellent support for prob & stat computations.

The Julia programming language provides an extensive mathematical function library, including support for probability distributions.

Lectures

Statistics 110: Probability by Joe Blitzstein at Harvard. 34 videos. ~50 minutes each. The best class on probability theory I've watched so far!

Probability and Statistics: an introduction by Norman J. Wildberger at UNSW. 8 videos. ~50 minutes each. The shortest class on probability theory I've enjoyed so far.

Math 131A: Introduction to Probability and Statistics by Michael Cranston at UC Irvine. The next OCW class I'm going to try to watch.

Dice rollers

Anydice

Dicelab

Troll dice roller and probability calculator

A miscellany of simulators, random generators and calculators

Chainmail Post Melee Morale - A JavaScript fiddle

Graphical OD&D combat simulator in NetLogo

Lots of random generation... - A discussion thread on these boards.

OD&D combat simulator in Perl

Palamedes - JavaScript dice roller, probability calculator, and Bayesian belief net. Alpha quality.

A list of probabilistic programming languages - A non-technical introduction to probabilistic programming. Figaro, a free PPL that runs on the JVM, and a 91-page PDF tutorial.

Procedural Dungeon Generation Algorithm

Viennese mazes - A Viennese maze is essentially a labyrinth in which passageways open and close in a periodic fashion. The linked page introduces the idea and provides a Python program for generating them.

[krusader74]

Review of standard probability theory

Here's a quick review of standard probability theory.

Definitions

• The sample space Ω is the set of all outcomes ω
• A σ-algebra ℱ ⊆ 2^Ω, called "events", satisfies:
• Ω ∈ ℱ
• ℱ is closed under complements: if A ∈ ℱ, then (Ω \ A) ∈ ℱ
• ℱ is closed under countable unions: if A_i ∈ ℱ for i=1,2,..., then (∪_i A_i) ∈ ℱ

[li]A probability measure P : ℱ → ℝ is a function that maps events to real numbers[/li]
[li]A probability space is the triple (Ω, ℱ, P)[/li]
[li]The probability that events A or B occur is the probability of the union of A and B: P(A ∪ B)[/li]
[li]The probability that events A and B both occur is the probability of the intersection of A and B: P(A ∩ B)[/li]
[li]Two events are mutually exclusive (or disjoint) if they cannot occur at the same time: P(A ∩ B) = 0[/li]
[li]The probability that event A occurs, given that event B has occurred, is called a conditional probability: P(A|B) = P(A ∩ B) / P(B)[/li]
[li]The complement of an event is the event not occurring: P(A') = P(Ω \ A), where the backslash \ means set difference and the apostrophe ' means complement[/li]
[li]If the occurrence of event A does not change the probability of event B, then events A and B are independent and P(A ∩ B) = P(A) · P(B). Otherwise, the events are dependent.[/li]
[/ul]
Example: When you roll a d6, the sample space is Ω = {1,2,3,4,5,6}. If we define ℱ = 2^Ω, then there are 2⁶ = 64 events, because each of the six outcomes is either in or out (two possibilities) of a given event. Examples of events include:

• No roll E_none = ∅
• A roll exactly equal to one E_one = {1}
• A roll of 5 or more E₅₊ = {5,6}
• An even roll E_even = {2,4,6}
• Any roll E_any = Ω

The probability measure is P(E) = |E|/6, where |E| is the number of outcomes in the event. The probabilities of the events listed above are

• P(E_none) = 0
• P(E_one) = 1/6
• P(E₅₊) = 1/3
• P(E_even) = 1/2
• P(E_any) = 1

Axioms

A probability measure P maps events to real numbers and satisfies the following three axioms:

1. Non-negativity: ∀ E ∈ ℱ P(E) ≥ 0.
2. Unitarity: P(Ω) = 1.
3. Countable additivity (or σ-additivity): P(∪^∞_i=1 E_i) = Σ^∞_i=1 P(E_i) if the E_i are mutually exclusive, i.e., E_i ∩ E_j = ∅ if i ≠ j.

Sometimes we're only interested in finitely additive probability spaces, in which case we replace the last axiom with

3'. Finite additivity: P(E₁ + E₂) = P(E₁) + P(E₂) if E₁ and E₂ are mutually exclusive, i.e., E₁ ∩ E₂ = ∅.

Rules

The following rules encapsulate the most important theorems deduced from the definitions and axioms:

• The probability of the empty set: P(∅) = 0
• Monotonicity: if A ⊆ B, then P(A) ≤ P(B)
• The numeric bound: 0 ≤ P(E) ≤ 1 ∀ E ∈ ℱ
• The complement/subtraction rule: P(A') = 1 - P(A)
• The chain/multiplication/product rule:
• P(A ∩ B) = P(A|B) · P(B)
• P(A ∩ B ∩ C) = P(A|B ∩ C) · P(B|C) · P(C)
• Etc.

[li]Bayes' rule: P(A|B) = P(B|A) · P(A) / P(B)[/li]
[li]The sum/addition/inclusion-exclusion rule:[/li]

• P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
• P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)
• Etc.

[li]The law of total probability:[/li]

• P(A) = P(A|B) · P(B) + P(A|B') · P(B')
• P(A|B) = P(A|B ∩ C) · P(C) + P(A|B ∩ C') · P(C')
• Etc.

[/ul]

[krusader74]

Exotic probabilities

Tinkering with the axioms

When we tweak the axioms of Euclidean geometry, we get non-Euclidean geometries. Euclid's fifth (or parallel) postulate says:

In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.[1]

If instead we assume there are no such parallel lines, then we get spherical geometry. And if instead we assume there are infinitely many parallel lines, then we get hyperbolic geometry.

So what happens when we tweak the axioms of standard probability theory? We get what's called Exotic probability.

The intent of this post isn't to present new research, but only to review the literature on exotic probability starting in 1930.

Non-unitarity

Let's first relax the axiom that probabilities sum to one. We'll look at a couple of real-life situations. The first example is adapted from lecture #2 in Donald Saari's 16-lecture course "Math 176: Math of Finance" given at UC Irvine. The second example is from lecture #3. (You can watch the whole course online here. The overall purpose of Saari's course is to develop the Black-Scholes equation and its solution, step-by-step, starting from first principles. It's a great online class if you're interested in math and finance and you want to see where this difficult PDE came from, what it means and how to work out its solution.)

Hedging example

The famous gladiator Aemilius Lepidus ("A" for short) is fighting in the gladiatora munera this weekend at the Forum Romanum.

The Gothic mercenary Hrœdberð ("Bob" for short) and the Egyptian grain trader sšn ("Sue" for short) have vastly different opinions as to who will win the game, and they are each willing to wager on the outcome.

Bob likes A to win the game. He is offering 5:3 odds. This means he will pay the gambler 5 gp for a 3 gp wager (and return the bettor his or her wager) in case A loses and nothing in case A wins. Sue thinks A will lose and offers 3:2 odds. You have 100 gp to bet with Bob and Sue.

Problem

1. How can you divide the 100 gp on wagers with Bob and Sue to ensure you always make money?
2. What amount do you wager with Bob (the rest being bet with Sue) to maximize your winnings?
3. What is this maximum amount that you win?

Solution

Bob thinks A will win. Let x be the amount you bet with Bob that A loses. Then (100 - x) is the amount that you bet with Sue that A wins. There are two cases to consider:

Case 1: If A wins, you lose x with Bob, but you win 3/2 (100 - x) from Sue. In this case, the profit curve is

-x + 3/2 (100 - x)

Case 2: If A loses, you win 5/3 x from Bob, but you lose (100 - x) with Sue. In this case, the profit curve is

5/3 x - (100 - x)

Part 1. Find the feasible region by setting each profit curve greater than zero. On WolframAlpha, you can do this by typing the command

solve -x + 3/2 (100 - x) > 0 && 5/3 x - (100 - x) > 0 for x

Click the Approximate form button to see the result as a decimal instead of a fraction:

Result: 37.5 < x < 60

Any amount wagered in this feasible region ensures you make a profit! Let WolframAlpha compute the feasible region now by clicking this link:

Part 2. Find the point in the range that maximizes your profit, by setting both profit curves equal

solve -x + 3/2 (100 - x) = 5/3 x - (100 - x) for x

The result is x = 1500/31. Press the Approximate form button once, then the More digits button twice. You get: x ≈ 48.3870967741935. Let WolframAlpha compute the feasible region by clicking this link.

Part 3. Find the maximum profit by substituting the value of x back into either one of the equations. For example:

solve p = 5/3 x - (100 - x) for p where x = 1500/31

Result: p = 900/31 ≈ 29.0323. Let WolframAlpha compute the feasible region by clicking this link.

Horse racing example

You manage a race track. The three horses Alduin, Bowrider and Curse ("A", "B" and "C" for short) are about to race. The total amount wagered on horse A is 600 gp, on B is 300 gp and on C is 100 gp. How do you fix the odds on A, B and C to ensure you make 30 gp regardless of the outcome?

Horse	Wagers	Odds	Profit curve (assuming given horse wins)
A	600 gp	X:1	-600 X + 300 + 100 = 30
B	300 gp	Y:1	600 - 300 Y + 100 = 30
C	100 gp	Z:1	600 + 300 - 100 Z = 30

Solve for X, Y, and Z. You can do this in WolframAlpha with the command

Solve[{-600 X + 300 + 100 == 30, 600 - 300 Y + 100 == 30, 600 + 300 - 100 Z == 30}, {X, Y, Z}]

Let WolframAlpha compute the feasible region by copying and pasting the command. The result is X = 37/60 and Y = 67/30 and Z = 87/10. In decimals: X ≈ 0.61667 and Y ≈ 2.2333 and Z ≈ 8.7000

Discussion

In gambling a Dutch book or lock is a set of odds and bets which guarantees a profit, regardless of the outcome of the gamble. It is associated with probabilities implied by the odds not being coherent.[2]

In the first example, your ability to profit no matter what happens springs from the fact that Bob and Sue's probabilities for the two different outcomes are incoherent: they sum to less than unity.

Bob thinks there are 5 ways A can win and 3 ways A can lose. Therefore, he thinks the probability A will lose is 3/(5+3) = 3/8.

Sue thinks there are 3 ways for A to lose and 2 ways for A to win. Therefore, she thinks the probability A will win is 2/(3+2) = 2/5.

So the probability that A loses plus the probability that A wins is P(A') + P(A) = 3/8 + 2/5 = 31/40 ≈ 0.775 < 1.

In the second case, where the bookmaker always wins, the sum of the probabilities P(A) + P(B) + P(C) = 37/(37+60) + 67/(67+30) + 87/(87+10) = 191/97 = 1.9690 > 1.

Generalizing this, I claim that any time the probabilities sum to less than 1, an individual gambler can always profit. Conversely, if the sum of the probabilities > 1, then the system is rigged against gamblers, and the bookmaker always profits.

Non-negativity

Next, lets relax the axiom that probabilities can't be negative. We'll look at a half-coin, described in the the paper "Half of a Coin: Negative Probabilities" by Gábor J. Székely:

Half coins are strange objects with infinitely many sides. They are numbered with 0,1,2,... and the positive even numbers are taken with negative probabilities. Two half coins make a complete coin in the sense that if we flip two half coins then the sum of the outcomes is 0 or 1 with 1/2 probability as if we simply flipped a fair coin.[3]

Székely developed the idea of a half-coin using probability generating functions.

Probability generating functions

A random variable X is just a function that maps an outcome to a real number, viz. X : Ω → ℝ. For example, the sample space for a coin toss is Ω = {heads, tails}. The random variable X that models a $1 payoff on a bet on heads is



Given a random variable X, its probability generating function G(x) = p₀ + p₁ x + p₂ x² + ... is a power series in the indeterminate x, whose coefficients p_n encode the probability mass function P(X=n).

For example, let X be the random variable for a fair coin described above. Its pgf is 1/2 x⁰ + 1/2 x¹ = (1 + x)/2

Key facts about pgfs:

1. If G is the pgf of a random variable X, then the sum of the probabilities is G(1).
2. If G is the pgf of an rv X, then the expected (mean) value of X is E[X] = G'(1) where the prime symbol (apostrophe) denotes taking the first derivative.
3. If G is the pgf of an rv X, then the variance of X is Var[X] = G''(1) + G'(1) - (G'(1))².
4. If G is the pgf of an rv X and H is the pgf of an rv Y, then G · H is the pgf of X + Y.

Half-coins

This last key fact implies that the pgf of a half-coin is the square root of the pgf of a fair coin, viz., √((1 + x)/2). We can use WolframAlpha to expand out this power series to get the coefficients:

series (1/2 x^0 + 1/2 x^1)^0.5

You should get results that look like this:



The referenced paper shows how to put the coefficients of this series into the following form: p_n = (-1)^n-1 √2 (C_n-1)/(4ⁿ) for n=0,1,2,..., where the C_n-1 are the Catalan numbers, i.e., sequence A000108 in the On-Line Encyclopedia of Integer Sequences.

Note that

1. there are an infinite number of coefficients. This means the half-coin has an infinite number of sides.
2. the probabilities p_n are negative for all positive even numbers n.

Half-coins don't really exist. So what use are negative probabilities? There are important applications to physics and finance.

Physics

Mark Burgin (2010)[4] pinpoints the genesis of negative probabilities in physics:

Negative probabilities emerged in physics in 1930s when Dirac (1930) and Heisenberg (1931) introduced probability distributions with negative values within the context of quantum theory... Wigner (1932) came to the conclusion that quantum corrections often lead to negative probabilities while he was supplanting the wavefunction from Schrödinger's equation with a probability distribution in phase space... Dirac (1942) not only supported Wigner's approach but also introduced the physical concept of negative energy. He wrote: "Negative energies and probabilities should not be considered as nonsense. They are well-defined concepts mathematically, like a negative of money."

Richard Feynman[5] offers the simplest explanation with his Roulette wheel example. Consider the following table of conditional probabilities:

Result X	Condition A	Condition B
1	0.3	-0.4
2	0.6	1.2
3	0.1	0.2

Notice that the conditional probability P(X=1|B) is negative. Feynman justifies this as follows:

It is not my intention here to contend that the final probability of a verifiable physical event can be negative. On the other hand, conditional probabilities and probabilities of imagined intermediary states may be negative in a calculation of probabilities of physical events or states.[6]

Now assume that P(A) = 0.7 and P(B) = 0.3. Then P(A) + P(B) = 1. We can calculate the probabilities of X as follows:

• P(X=1) = P(X=1|A) · P(A) + P(X=1|B) · P(B) = 0.3 · 0.7 - 0.4 · 0.3 = 0.09
• P(X=2) = 0.78
• P(X=3) = 0.13

So even though the conditional probability P(X=1|B) is negative, (∀ i) P(X=i) ≥ 0 and ∑_i=1³ P(X=i) = 1, just as expected in standard probability theory.

Feynman explains that if you calculate a negative probability, you may interpret it to mean:

1. the initial conditions can't be realized in the physical world, or
2. the situation can't be observed directly

Heisenberg Uncertainty

More importantly for physics, if you calculate two correlated probabilities such that one is always positive when the other is negative, then it means you can't measure one situation at the same time as you measure the other. For example, Feynman gives us values of P(A) and P(B) such that

• P(X=1) ≥ 0 whenever P(X=3) < 0 and
• P(X=1) < 0 whenever P(X=3) ≥ 0

This means you can't measure 1 at the same time you measure 3. Feynman comments:

This is reminiscent of the situation in quantum mechanics in relation to the uncertainty principle.[7]

Non-unitarity revistited

Feynman sees a relationship between negative probabilities and non-unitarity:

A probability greater than unity presents no problem different from that of a negative probabilities, for it represents a negative probability that the event will not occur.[8]

Extended Probabilities

Mark Burgin[9] provides an axiomatization of negative probabilities. Without getting into details, the basic idea is to partition the sample space into positive Ω⁺ and negative Ω^- parts such that the probability of an event occurring with its anti-event is zero. In symbols:

(∀ ω ∈ Ω⁺) (∃ -ω ∈ Ω^-) P({ω, -ω}) = 0

In other words, negative probabilities provide a convenient framework for letting us write down that two things can't happen together, like measuring a particle's position and momentum at the same time.

Finance

In finance, Macaulay duration is the weighted average maturity of cash flows. Since the cash flows may be positive or negative, we can re-interpret the formula for duration as the expected value of a probability distribution whose probabilities may be negative. Székely does this in his paper on the half-coin.

---

[1]: Parallel postulate. In Wikipedia, The Free Encyclopedia.
[2]: Dutch Book. In Wikipedia, The Free Encyclopedia.
[3]: Gábor J. Székely, Half of a Coin: Negative Probabilities, Wilmott Magazine (July 2005), pp. 66--68:
[4]: Mark Burgin. Interpretations of Negative Probabilities (2010)
[5]: Richard P. Feynman, Negative Probability (1987)
[6]: Ibid., p. 4
[7]: Ibid., p. 6
[8]: Ibid., p. 3
[9]: Mark Burgin, Extended Probabilities: Mathematical Foundations (2009)

[Deleted]

Now that is quite a resource! Have an Exalt!

[Finarvyn]

The first couple of posts are awesome, but I'll confess that as I continued down the thread I started to get all glassy-eyed. More probability than I have time to ponder, I suspect, but I love the idea of looking at probabilities and wish I had the time to study the topic further.

Part of my problem with probabilities is that I never really learned the theory to the level that I ought, but instead most of my probability calculations are done by a "brute force" method of creating tables and counting outcomes. Not so elegant, but works for a lot of what I need.

[krusader74]

Hot-hand fallacy dice

A study was conducted to examine the difference between the hot-hand and gambler's fallacy. The gambler's fallacy is the expectation of a reversal following a run of one outcome. Gambler's fallacy occurs mostly in cases in which people feel that an event is random, such as rolling a pair of dice on a craps table or spinning the roulette wheel. It is caused by the false belief that the random numbers of a small sample will balance out the way they do in large samples; this is known as the law of small numbers heuristic. The difference between this and the hot-hand fallacy is that with the hot-hand fallacy an individual expects a run to continue. --Wikipedia

What follows is a "show and tell" about some computer code I'm writing this week. I am re-writing and expanding Evan Verworn's Gambler's fallacy Dice, an ES6 (JavaScript) class for dice that follow the Gambler's fallacy.

In addition to Gambler's fallacy dice in which people tend to predict the opposite outcome of the last event (negative recency), it also implements Hot-hand fallacy dice in which people tend to predict the same outcome of the last event (positive recency). (It implements a fair die too!)

It adds convenience functions for making tables of probabilities, summarizing sample statistics, and performing Chi-squared hypothesis testing. It uses ESDoc to document the API.

I still have a liitle more work to do (see the Future research section near the end). When I'm done, I'll post the finished product on GitHub, which is having some problems with outages this week. I've attached the source code at the bottom, in case someone wants to try it now. (It works!)

The following demonstration should help explain what this is all about...

Demo

Included in the source code is a script that demonstrates the main features. In the project's root directory, run the script from the command line by entering:

$ node -r markdown-table -r chi-squared-test -r ./src/Dice ./src/dice-demo.js

or more simply as

$ npm run demo

The resulting MarkDown-formatted output looks like this...

hot-hand-dice demo

We will be rolling three kinds of dice and testing them for fairness using Pearson's chi-squared test:

• a fair die
• a die that follows the gambler's fallacy (negative recency)
• a die that follows the hot-hand fallacy (positive recency)

The null hypothesis H₀ is that all faces are equally likely. The significance level α (alpha) is 0.001. We roll each die 10,000 times, compute the p-value as p = 1 - F(χ²₅), and reject H₀ if p ≤ α.

FairDie

Roll 10 times and show the probability distribution for all 10 and the next...

Roll	% of 1	% of 2	% of 3	% of 4	% of 5	% of 6	Actual Roll
1	16.7	16.7	16.7	16.7	16.7	16.7	2
2	16.7	16.7	16.7	16.7	16.7	16.7	2
3	16.7	16.7	16.7	16.7	16.7	16.7	1
4	16.7	16.7	16.7	16.7	16.7	16.7	5
5	16.7	16.7	16.7	16.7	16.7	16.7	3
6	16.7	16.7	16.7	16.7	16.7	16.7	3
7	16.7	16.7	16.7	16.7	16.7	16.7	1
8	16.7	16.7	16.7	16.7	16.7	16.7	3
9	16.7	16.7	16.7	16.7	16.7	16.7	3
10	16.7	16.7	16.7	16.7	16.7	16.7	4
11	16.7	16.7	16.7	16.7	16.7	16.7	?

Roll once: 5

Generate sample of size 3: 5,5,5

Generate sample of size 9,986 (not shown) for a total of 10,000 rolls so far...

Generate sample statistics for all 10,000 rolls...

Statistic	Value
sample size N	10000
sample mean m	3.49
sample standard deviation s	1.71
% of 1	16.83
% of 2	16.30
% of 3	17.18
% of 4	16.92
% of 5	16.07
% of 6	16.70

p-value: 0.406724960090882 (not significant: do not reject the null hypothesis that all faces are equally likely)

GamblersDie

Roll 10 times and show the probability distribution for all 10 and the next...

Roll	% of 1	% of 2	% of 3	% of 4	% of 5	% of 6	Actual Roll
1	16.7	16.7	16.7	16.7	16.7	16.7	4
2	18.2	18.2	18.2	9.1	18.2	18.2	4
3	18.8	18.8	18.8	6.3	18.8	18.8	1
4	5.3	21.1	21.1	10.5	21.1	21.1	2
5	9.5	4.8	23.8	14.3	23.8	23.8	4
6	12.5	8.3	25.0	4.2	25.0	25.0	6
7	16.7	12.5	29.2	8.3	29.2	4.2	5
8	21.7	17.4	34.8	13.0	4.3	8.7	1
9	4.2	20.8	37.5	16.7	8.3	12.5	3
10	9.5	28.6	4.8	23.8	14.3	19.0	1
11	4.0	28.0	8.0	24.0	16.0	20.0	?

Roll once: 2

Generate sample of size 3: 5,3,6

Generate sample of size 9,986 (not shown) for a total of 10,000 rolls so far...

Generate sample statistics for all 10,000 rolls...

Statistic	Value
sample size N	10000
sample mean m	3.51
sample standard deviation s	1.71
% of 1	16.48
% of 2	16.82
% of 3	16.37
% of 4	17.08
% of 5	16.49
% of 6	16.76

p-value: 0.8290540016036037 (not significant: do not reject the null hypothesis that all faces are equally likely)

HotHandDie

Roll 10 times and show the probability distribution for all 10 and the next...

Roll	% of 1	% of 2	% of 3	% of 4	% of 5	% of 6	Actual Roll
1	16.7	16.7	16.7	16.7	16.7	16.7	1
2	28.6	14.3	14.3	14.3	14.3	14.3	6
3	25.0	12.5	12.5	12.5	12.5	25.0	3
4	22.2	11.1	22.2	11.1	11.1	22.2	3
5	20.0	10.0	30.0	10.0	10.0	20.0	1
6	27.3	9.1	27.3	9.1	9.1	18.2	1
7	33.3	8.3	25.0	8.3	8.3	16.7	1
8	38.5	7.7	23.1	7.7	7.7	15.4	6
9	35.7	7.1	21.4	7.1	7.1	21.4	3
10	33.3	6.7	26.7	6.7	6.7	20.0	1
11	37.5	6.3	25.0	6.3	6.3	18.8	?

Roll once: 3

Generate sample of size 3: 4,1,3

Generate sample of size 9,986 (not shown) for a total of 10,000 rolls so far...

Generate sample statistics for all 10,000 rolls...

Statistic	Value
sample size N	10000
sample mean m	3.31
sample standard deviation s	1.80
% of 1	30.92
% of 2	0.17
% of 3	22.73
% of 4	9.79
% of 5	25.81
% of 6	10.58

p-value: 0 (significant: reject the null hypothesis that all faces are equally likely)

Things to notice about the demo

• The gambler's die has the same statistical properties as the fair die: same mean, standard deviation, and (in the long run) the same probability distribution.
• In the statistical tests, the gambler's die tends to produce higher p-values than the fair die (which equates with lower χ² test statistics).
• The hot-hand fallacy is related to the Matthew Effect: "The rich get richer, and the poor get poorer (Mt. 25:29)" and the Simon Model. Success tends to flow to those who experience a little early success.
• The limit of the pmfs of the hot-hand die almost surely converge to a discrete power-law distribution, i.e., f(x)=a x^-k for some permutation x of the faces. Note that a power-law distribution only has a well-defined mean if k>2, and it only has a well-defined variance if k>3.

Future research

First, it is most likely that the hot-hand die does not possess a well-defined mean or variance! What needs to be done is an estimation of the exponent of discrete power law data.

Second, I want to implement a die that follows the Simon Model. Such a die generally works like a hot-hand die, except that on each roll there is a tiny probability that the die "grows" a new face! This kind of die also follows a discrete power law.

Lastly, the number of rolls (10,000) in the demonstration was arbitrary. What really needs to be done:

1. Experimentation to find the effect size w = √(χ²₅/n) for fair dice rolls. For a general χ² distribution, the rule of thumb is 0.5 is a large effect size, 0.3 moderate, and 0.1 small. In the articles I reviewed (see the references below), it is generally assumed when we test dice we're looking for a large effect size (0.5). That assumption should be tested.
2. A function N that maps significance (α), statistical power (1 - β) and effect size (w) to sample size N = N(α, 1 - β, w).

References

Here are some references that go into more detail about testing dice for fairness as well as the relationship between sample size, effect size, statistical power and significance level for χ² distributions:

• Testing Balanced Dice Power - Delta's D&D Hotspot
• Mathematical tests for fair dice - timothyweber.org
• How many rolls do I need to determine if my dice are fair? - StackExchange
• Power of Chi-square Tests - Charles Zaiontz, Real Statistics Resources
• Effect Size for Chi-square Test - Charles Zaiontz, Real Statistics Resources
• Power Calculation for Chi-Square Test
• Power Analysis in R

Appendices

Dependencies

To run the source code, you will need:

• ES6/ES2015 JavaScript engine - I use Nodejs v8.2.1
• chi-squared-test for statistical hypothesis testing
• markdown-table for formatting arrays as MarkDown tables

Development dependencies

To continue development of this code, you should also have:

• ESLint for ES6 linting, run with npm run lint
• ESDoc for documentation, run with npm run doc
• Tape for testing, run with npm run test

Attachments

hot-hand-dice.zip (476.88 KB) - ZIP archive with all source code, documentation and tests

[krusader74]

How many times must you roll a die to test for fairness?

I see this question raised a lot. But so far, I haven't seen a thoroughly satisfying answer. So I decided to try and write one...

Effect size

Problem: Too many statistical studies fetishize an arbitrary 0.05 significance level (alpha) such that a p-value of 0.04999 is a publishable finding but p=0.05001 is not. The big problem with this is that even the most trivial effect will eventually become statistically significant if you test enough (because: the law of large numbers).

Solution: The solution to this problem is a system for deciding precisely how large the effects in our data really are. In statistics, the effect size is used to describe a difference between two groups.

Calculating effect size

Each type of statistical test has its own way of calculating effect size.

When we test dice for fairness, we typically use Pearson's chi-squared (χ²) test, a type of Goodness of Fit test (of which there are many). The measure of effect size used for chi square tests is Cohen's w, defined as:



Here the p_0i refer to the probabilities under the Null Hypothesis H₀, and the p_1i refer to the probabilities under the Alternative Hypothesis H₁.

Example: You throw a six-sided die a bunch of times to test for unbiasedness. The Null Hypothesis H₀ says that p_0i=1/6 for i=1 to 6. The Alternative Hypothesis H₁ says that the p_1i ≠ p_0i for some of the i's.

Remark 1: to actually compute w, we need concrete values for the p_1i, e.g., the die is loaded and the probability of throwing a six is 1/4 and the other sides are equiprobable.

Remark 2: The null hypothesis states what's commonly assumed to be true. When we test a die for fairness, we generally assume all sides are equally probable. So if you're testing a d20 for faireness, then H₀: p_0,i=1/20 for i=1 to 20. However, if you happen to manufacture loaded d20s such that the "20" appears 10% of the time and the "1" never appears, and you want to test your loaded dice for quality control, then your null hypothsis won't be equiprobability. Instead it will be H₀: p_0,1 = 0, p_0,i = 1/20 for i in 2 to 19, and p_0,20 = 1/10.

What is meant by "small" and "large" effect sizes?

In Cohen's terminology, a "small" effect size is one in which there is a real effect --- something is really happening in the world --- but which you can only see through careful study. A "large" effect size is an effect which is big enough (or consistent enough) that you may be able to see it "with the naked eye." The following table summarizes what is meant by "small" and "large" in terms of Cohen's w:

Type of effect	Effect Size (w)
trivial effect	< 0.10
small effect	≈ 0.10
moderate effect	≈ 0.30
large effect	> 0.50

Example: You throw a six-sided die a bunch of times to test for unbiasedness. If the die is really unfair and the percentage of times each face appears is given by the following table, then it has the effect size shown in the last column:

Type of effect	% of 1s	% of 2s	%of 3s	% of 4s	% of 5s	% of 6s	Effect Size (w)
trivial effect	14.27	16.67	16.67	19.07	16.67	16.67	0.083138
small effect	18.60	14.40	16.80	18.00	14.20	18.00	0.105451
moderate effect	14.70	20.70	16.50	7.10	21.00	20.00	0.291452
large effect	0.00	23.60	23.60	11.80	21.00	20.00	0.506454
(very!) large effect	3.30	0.00	93.30	0.00	0.00	3.40	2.058253

Power

Power and sample size estimations are used to determine how many observations are needed to test the null hypothesis against an alternative. There are two types of errors we can make in a statistical study:

• A type I error is said to have occurred when we reject the null hypothesis incorrectly. The significance level (or "alpha") is the probability of making a type I error, i.e., α = P(reject H₀ | H₀ is true). Note: alpha is a conditional probability, and there are many common fallacies concerning them.
• A type II error is said to occur when we fail to reject the null hypothesis incorrectly. The chance ("beta") of making a type II error is β = P(fail to reject H₀ | H₁ is true).

The power of a test is the probability that the test correctly rejects the null hypothesis when the alternative hypothesis is true. Mathematically, power is defined as 1 - β = P(reject H₀ | H₁ is true). It is the complement of beta. Note: Each type of statisical test has its own method for computing power (and/or beta).

In Pearson's chi-squared (χ²) test, the formula for power (and/or beta) is (**)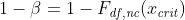



where

• F is the is the cumulative distribution function (cdf) for the noncentral chi-square distribution
• nc is the noncentrality parameter of the noncentral chi distribution. It is defined as nc = n * w², where n is the sample size and w is the effect size.
• df are the degrees of freedom for the test. E.g., when you throw a six-sided die under a given hypothesis which defines the probability distribution, then df=5 because knowing 5 of these probabilities determines the sixth.
• x_crit is the critical value for the given value of alpha, i.e.,

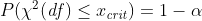Sample Size

To determine the sample size required to test for an unbiased die, follow these steps:

1. Decide the significance level α. By convention, this is usually chosen to be 0.05, 0.01 or 0.001.
2. Decide the power 1 - β. By convention, this is usually chosen to be 0.80 or 0.90.
3. Decide the effect size w you want your test to detect.
4. Solve the above equation (**) for n.

The last step would be extremely difficult to compute by hand, given the complexity of the noncentral chi distribution. There are many solvers freely available online.

I've written my own free, public domain Python module (chisq.py) to do the math. It computes:

• Effect size w, given Alternative Hypothesis (and optional Null Hypothesis, assumed to be equiprobable outcomes by default)
• Power 1 - β, given w, n, df (and optional alpha, assumed to be 0.05 by default)
• Sample size n, given w, df (and optional alpha (0.05 by default) and power (0.80 by default))

The script requires the scipy.stats and scipy.optimize libraries. There's actually very little code in the script, since scipy does all the heavy lifting. If I find a decent JavaScript library that computes the noncentral chi distribution (or write my own someday...), then I will write a JavaScript version of these functions and put them online as a jsfiddle.

[foxroe]

A fascinating thread as usual krusader74 , even if a bit over my head at times (and I'm an engineer!).

A query, if you will (and this may already be answered up-thread)...

I'm thinking about a 3d6 sum roll-under mechanic where bonuses and penalties are applied with additional dice (usually one die, but sometimes two, and rarely three). In a bonus situation, (3+x)d6 are rolled, and the lowest three die are totaled. In a penalty situation, (3+x)d6 are rolled, and the highest three die are totaled. Hopefully that's clear.

Now my question is, what would be the probability distribution of the 3-18 results in each case? I'm trying to determine if the "fiddliness" of the mechanic is offset by significant changes in the bell curve, or if I would be better off sticking with a simpler 3d6+x method.

I tried looking into your Palamedes program, but I couldn't figure out what code to input to simulate the conditions.

[sixdemonbag]

Sept 12, 2017 19:34:38 GMT -6 foxroe said:

Now my question is, what would be the probability distribution of the 3-18 results in each case?

anydice.com/program/cea2

Click "At Most" to get chances of success or "At Least" for chances of failure in your roll under system (it would be reversed in a roll over system).

EDIT: Try the link again. I made some goofs. 

[sixdemonbag]

Updated link in previous post to reflect changes.

[foxroe]

Sept 12, 2017 23:53:12 GMT -6 sixdemonbag said:

Sept 12, 2017 19:34:38 GMT -6 foxroe said:

Now my question is, what would be the probability distribution of the 3-18 results in each case?

anydice.com/program/cea2

Click "At Most" to get chances of success or "At Least" for chances of failure in your roll under system (it would be reversed in a roll over system).

EDIT: Try the link again. I made some goofs. 

Sweet, exactly what I wanted! Thanks!

Hmmm. It's not as elegant as I expected. The jump from 3d6 to 3d6+1d6 is significant, 3d6+2d6 less so, and 3d6+3d6 is negligibly different from 3d6+2d6. It makes a bigger difference at the extremes of the scale. I'll have to look into this some more and see how it compares to a straight 3d6+x mechanic.

[foxroe]

OK, so...

Using the "anydice" program to compare the two mechanics (a roll-under 3d6+xd6 pool mechanic versus a straight 3d6+x mechanic), it seems that in the dice pool mechanic, extra dice provide slightly more "bonus" for the first two dice, with successive die additions providing diminishing returns.

However, I foresee issues with using it in actual play:
- Negative bonuses and positive penalties may be non-intuitive for some players.
- Players will likely find it easier to roll 3d6 and add or subtract a few points, than to roll a handful of dice and hunt for the three lowest/highest die.
- Adding/subtracting points encourages more "spread", while adding more dice causes headaches (a subjective opinion, of course).

And now back to your regularly scheduled thread.

[sixdemonbag]

People have trying to make dice pools happen for decades. It's always the sexy option. But, in my limited experience, linear probabilities just flow better at the table and from a design perspective.

Now, d100 is overkill to me (the very best humans can't discern much less than 1.5 normal cumulative variation or about 6.6% (VERY close to the d20 5% granularity). This is why the d20 is perfect. If you rolled a d20 30 times and announced "success" every time a 15 or higher was rolled, then did the same thing with a 14 or highter, would you be able to to pick out the subset of rolls that succeeded more often? Well in this case some people might be able to but not most. This puts the d20 right on the edge of human awareness which is perfect. Almost nobody could tell the difference between event A occurring 66% of the time and event B occurring 67% of the time. 1% is just too granular for humans.

Single d6 rolls match up with 0.5 normal distribution intervals almost perfectly which is an amazing coincidence. This is why the d6 gets so much love. It's the best die for everyday modelling and observations. The five degrees of nonzero granularity that a d6 provides fits the way nature works the best. I believe that we humans can sense that somehow with the d20 approaching our limits of casual observation.

Thus, straight d20 and d6 rolls hit the sweet spot for me. If your design is made so that the pool size never changes (monopoly, yahtzee, reaction checks, etc.) and the extremes aren't much less 6.6% then they can work out great. So maybe don't give up quite yet.

[sixdemonbag]

For reference:

Cumulative normal distributions in 0.5 intervals: 16% 31% 50% 69% 84%

Compared to d6: 17% 33% 50% 67% 83%

That's a d**n near perfect match!!!

[krusader74]

Sept 12, 2017 19:34:38 GMT -6 foxroe said:

I'm thinking about a 3d6 sum roll-under mechanic where bonuses and penalties are applied with additional dice (usually one die, but sometimes two, and rarely three). In a bonus situation, (3+x)d6 are rolled, and the lowest three die are totaled. In a penalty situation, (3+x)d6 are rolled, and the highest three die are totaled. Hopefully that's clear.

Now my question is, what would be the probability distribution of the 3-18 results in each case?

Really great question, foxroe !!

sixdemonbag already posted a very practical answer, using anydice.com. So let me try to provide additional theory and some computational alternatives, since I'm sure others will ask questions about this same distribution in the future.

The probability mass function f(x) of the sum of the k-highest of n s-sided dice is given by an extremely unwieldy combinatoric formula:



where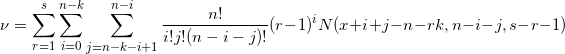



and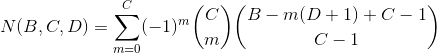



The formula was derived by a user called "techmologist" on Physics Forums. To see the step-by-step derivation of this formula along with further explanation and analysis, please read the linked 2-page article:

• techmologist.pdf (PDF)
• techmologist.tex (LaTeX source)

But this only answers part of your question, because

• you also want the distribution for rolling n s-sided dice and keeping the lowest k
• you really want the cdf, not the pmf, since you're thinking about a "roll-under mechanic"

To answer these two concerns succinctly:

First: The pmf for rolling n s-sided dice and keeping the lowest k looks like the mirror image of the pmf for rolling n s-sided dice and keeping the highest k. For example, the pmf g for rolling 4 6-sided dice and keeping the lowest 3 looks like the pmf f for rolling 4 6-sided dice and keeping the highest 3 after you swap the 18 with the 3, swap the 17 with the 4, and so on. In other words if π is the permutation: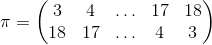



then

g = f ∘ π

Note that π is an involution, i.e., π∘π= 1 or equivalently π=π^-1, so that f=g∘π too.

Second: If f(x) is the pmf of the discrete random variable X, then its cdf is

F(x) = P(X ≤ x) = ∑_t≤x f(t)

If you were a masochist, you could write out the cdf F(x) for 4d6k3 in full to see what it looks like. It looks ugly. Very, very ugly. You'd see (among other things), five nested summation symbols. You really want a computer to manipulate these functions for you...

Sept 12, 2017 19:34:38 GMT -6 foxroe said:

I tried looking into your Palamedes program, but I couldn't figure out what code to input to simulate the conditions.

Not your fault! Palamedes is highly idiosyncratic. For example, you can't use the letter "x" as a variable name, because it is the syntax for an exploding die. Furthermore, Palamedes isn't finished or fully debugged yet. Nevertheless, you can get the Prob & Stat data you need from it, because it implements techmologist's formula. Here are some input examples:

   4d6k3 /* generate a random variate */
   cdf(4d6k3) ∘ 18 /* evaluate cdf at 18, returns 1 */
   p(4d6k3 ≤ 18) /* same as above, only more pleasing notation */
   table(p(4d6k3)) /* table for the pmf */
   table(cdf(4d6k3)) /* table for the cdf */
   table(QQ(cdf(4d6k3))) /* table for the cdf as fractions, not decimals */
   table(stats(p(4d6k3))) /* mean, variance, etc. */
   barchart(p(4d6k3)) /* plot of the pmf */
   barchart(cdf(4d6k3)) /* plot of the cdf */
   perm <- [3..18] -> [18..3] /* the permutation shown above */
   roll_4d6_keep_lowest_3 <- p(4d6k3) ∘ perm /* explained above */
   p(roll_4d6_keep_lowest_3 ≤ 18) /* cdf, returns 1 */
   p(roll_4d6_keep_lowest_3 ≤ 3)
   p(roll_4d6_keep_lowest_3 < 0) /* returns 0 */
   table(roll_4d6_keep_lowest_3)
   table(cdf(roll_4d6_keep_lowest_3))
   table(stats(roll_4d6_keep_lowest_3))
   barchart(roll_4d6_keep_lowest_3)
   barchart(cdf(roll_4d6_keep_lowest_3))

And here is the (really long...) output from running this script:



You can PM me with follow-up questions. Anyway, I hope this helps!

[sixdemonbag]

You are making us all look bad krusader74 ! Lol, very nice walkthrough there. I don't understand it all but it's really cool of you laying things out like that. Above and beyond!

[foxroe]

[krusader74]

Are dice throws predictable?

Dice throws are deterministic mechanical systems. But determinism does not imply predictability: They may be chaotic, in which case, a small, immeasurable perturbation in the initial conditions would lead to drastically different, unpredictable outcomes. To answer this question, you first write out the equations of motion for dice being thrown and bouncing on a surface. I won't bore you with the equations... you can see them in the references at the end. These equations merely encapsulate the physical laws governing the system:

1. Conservation of mass
2. Conservation of energy (potential + kinetic)
3. Conservation of momentum (translational and angular)

Then you check for sensitive dependence on initial conditions: Do trajectories with different initial conditions separate exponentially? In the case of dice, it turns out the answer to this question is NO, as shown in the following two papers:

1. Dice Throw Dynamics Including Bouncing (XXIV Symposium Vibrations in Physical Systems, 2010) by Juliusz Grabski, et al. Quote:

It is shown that from the point of view of dynamical systems dynamics of die is predictable.

2. Iterated-map approach to die tossing (Physical Review A, Volume 42, No 8, 1990) by R. Feldberg, et al. Quote:

...the system has finite sensitivity to initial conditions.

[waysoftheearth]

Sept 13, 2017 3:10:33 GMT -6 sixdemonbag said:

For reference:

Cumulative normal distributions in 0.5 intervals: 16% 31% 50% 69% 84%

Compared to d6: 17% 33% 50% 67% 83%

That's a d**n near perfect match!!!

Agree it's "near enough" to be interesting, but what do you suggest is its utility?

Okay, so I kinda get that instead of throwing 600 weird-shaped dice I could boil them all down to 1d6 and then confidently declare: "A two! This implies our 600 throws would have yielded a result between 1 and 0.5 standard deviations below the mean." but... unless I've already got a credible sample of outcomes for the 600 dice thing I want to abstract (e.g., combat?) to a single d6, does this help much?

Happy to be educated

[sixdemonbag]

Mar 21, 2019 22:40:12 GMT -6 waysoftheearth said:

Agree it's "near enough" to be interesting, but what do you suggest is its utility?

Oh boy, you are asking the wrong person for any actual utility!

Going back and rereading this thread, I think it was nothing more than idle curiosity. However, now that you have me thinking, you could build an entire game (let's say an RPG) around a single d6 throw and it would feel somehow "natural."

So, in theory, you could boil down a lot the progression tables and such into a simple:

Players succeed/hit/save on a 3 or higher and monsters succeed/hit/save on a 5 or higher. No other bonuses besides the purely situational would be strictly necessary for an entire campaign.

An evil thought experiment:

1. Get an online game of D&D going where the ref makes all the rolls
2. For every PC action, hit, or save, just roll a d6 to determine success. Let's say 4 in 6, maybe adjusted by situation.
3. Don't tell them you are doing this, let them assume that you are using d20's and class tables.
4. For monsters, cut this in half and assume they succeed, hit, or save with 2 in 6 odds.
5. Do you think the players will ever notice?
6. Will they have fun?
7. Did this provide enough variety of outcome and yet still feel satisfying and not totally predictable at the same time?
8. Did this provide any actual surprises that enhanced the fun and excitement?

My hypothesis is that this type of set-up would actually be fun to play and provide enough randomness and a sense of player "competency" to be fun. Maybe the exact odds would need to be adjusted, but with a d6 modeling nature so closely, this would feel pretty natural no matter which direction you went in. You could do this with any die, of course, but with the d6, the math is already done for you, with just enough granularity to not be noticeable.

Now, there's really no practical reason to do this, but some enterprising game designer could take these principles and make a simple and fun game out of it. You could use the d6 and take advantage of casino slot machine variable ratio schedules to find the maximum addictive odds of success.

Using human psychology, for instance, most slot machines are programmed so that 9-25% of pulls are "winners." Less than this and players get frustrated at leave. More than this, and the payout has to be too small to attract further longterm play. For an RPG, it would be curious what the best VR (mean number of die throws per success) for addictive play turns out to be. I believe WOTC did some research via playtests and found it to be around 65-70% (I can't seem to find a link anywhere but I swear I read somewhere that they did this research???), otherwise the players felt like they were "missing" too often. This happens to be very close to 4 in 6 as above and reversed as 2 in 6 for monsters. Something about being right around a std. dev. seems to just "feel right."

This is long and rambling, so I apologize in advance for the wasted electrons...