Analysis of OD&D treasure types

[robertsconley]

Analysis of OD&D (original booklets only) treasure types.

Looking at the Original D&D treasure we see the following

B,C,D, E, & F are in order of increasing value. Although D&E are roughly equivalent, D has less potential value

but greater odds, while E has greater potential odds but lesser odds.

A, G, H, I are all all special treasure basically assigned to only one monster each.

A: Men & Centaur and is divided into Land, Desert, Water subcategories.

B:Skeletons, Zombies, Wights, Hydras, Nixies

C: Ogres (+1,000 GP), Gargoyles, Lycanthropes, Minotaurs, Pixies, Gnomes

D:Orcs, Hobgoblins, Gnolls, Mummies, Cockatrices, Manticoras, Purple Worms, Dryads

E:Giants (+5,000 GP), Wraiths, Spectres, Gorgons, Wyverns, Elves, Griffons

F:Vampires, Basiliks, Medusae, Chimera

G:Dwarves

H:Dragons

I:Rocs

[Stormcrow]

I came up with the same analysis once. The only thing I could conclude was that treasure types were assigned in a fairly offhand manner.

[Deleted]

Aug 8, 2012 11:18:23 GMT -6 Stormcrow said:

I came up with the same analysis once. The only thing I could conclude was that treasure types were assigned in a fairly offhand manner.

Ding! Winner.

Okay, we're done here. Somebody get me a beer.

[Sean Michael Kelly]

Aug 8, 2012 20:13:53 GMT -6 @gronanofsimmerya said:

Okay, we're done here. Somebody get me a beer.

Ditto! A pint or two of stout!

[talysman]

There are a couple other interesting bits. If you look at the magic items, Type F is weighted towards stuff that appeals to magic-users. I think of the H in Type H as standing for Hoard, and it seems to be designed around what you might expect in a dragon hoard. Type G, similarly, is weighted towards lots of gold. Type I is what I refer to as Incidental Treasure -- exactly the sort of stuff a roc or similar creature might snatch and return to its nest; thus, no coins, but jewelry, gems, and maybe a magic item.

Monsters in Greyhawk and Blackmoor get similarly appropriate treasures, but I think these relationships were too obscure for other monster creators, so people who studied the AD&D version of the table first didn't catch on to these patterns.

[waysoftheearth]

Some further analysis, for the totally obsessive ;D

Here is a table of the mean net worth for each treasure type:
(Excluding maps and magic items -- possibly the most valuable part of any hoard).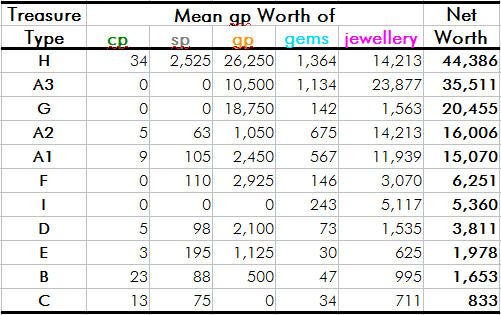




So the able treasure hunter will see right away that he is best served by going after pirates, buccaneers and mermen (type A3), and dwarves (type G) since these are only 1 HD monsters and have the richest hoards after dragons (type H). And dragons are a lot scarier!

You may note also that jewellery makes up the majority of the mean net worth of almost every treasure type (excepting type G). So, if you don't roll jewellery it's pretty likely the remainder of the hoard will be worth nix

To illustrate this point, here is a summary of the % net worth of each component in any treasure type (again excluding maps and magic items):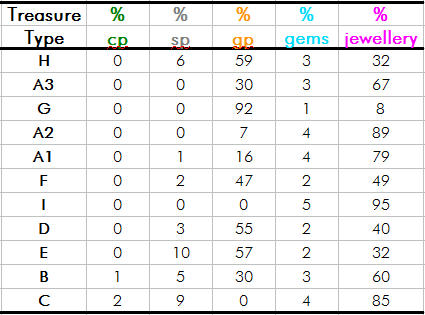




The reason that jewellery makes up such an overwhelming proportion of any treasure's net worth is that pieces of jewellery occur equally frequently as do gems, even though jewellery is over 20 times more valuable than are gems. (Gems are worth a mean of 55 gp each, while a piece of jewellery is worth an average of 1,137 gp).

This can make treasures pretty miserly if you just happen to not roll any jewellery a few times. However, the problem was "addressed" (to some extent) in AD&D, where the amount of jewellery occurring was approximately halved. Personally, I would have preferred if it was quartered! But it's your game -- so do as YOU please.

Enjoy

[robertsconley]

Aug 8, 2012 11:18:23 GMT -6 Stormcrow said:

I came up with the same analysis once. The only thing I could conclude was that treasure types were assigned in a fairly offhand manner.

Yes they are, the point of doing isn't to figure out why the monsters were assigned what treasure type. But what the treasure types themselves means. For example H is obviously a Hoard type of treasure. A is limited to men (and centaurs) while B to F are obviously a rough ascending scale.

Doing this allows an equivalent to be crafted for Swords & Wizardry or another retro-clone.

[waysoftheearth]

Aug 8, 2012 10:02:21 GMT -6 robertsconley said:

B,C,D, E, & F are in order of increasing value. Although D&E are roughly equivalent, D has less potential value but greater odds, while E has greater potential odds but lesser odds.

Aug 9, 2012 5:08:21 GMT -6 robertsconley said:

B to F are obviously a rough ascending scale.

I'm not sure how you are concluding this Robert..? The way I see it, it's more like:

C < B < E < D < F

to a value ratio something like this:

1 : 2 : 2.5 : 5 : 8

Unless I'm calculating the numbers differently to you, somehow?

[robertsconley]

Aug 9, 2012 5:27:55 GMT -6 waysoftheearth said:

Aug 8, 2012 10:02:21 GMT -6 robertsconley said:

B,C,D, E, & F are in order of increasing value. Although D&E are roughly equivalent, D has less potential value but greater odds, while E has greater potential odds but lesser odds.

Aug 9, 2012 5:08:21 GMT -6 robertsconley said:

B to F are obviously a rough ascending scale.

I'm not sure how you are concluding this Robert..? The way I see it, it's more like:

C < B < E < D < F

to a value ratio something like this:

1 : 2 : 2.5 : 5 : 8

Unless I'm calculating the numbers differently to you, somehow?

I saw it as basically C, B, D/E, F. D has greater potential treasure but a lower probability than E. I am not sure the best way of factoring in the odds. If your analysis did then I agree with you. Then the progression is B, C, E, D, F as you noted.

[robertsconley]

The end results that for an OD&D clone that want to use treasure type the setup would be something like this.

Men, Normal (land) Hoard
Men, Dervish/Nomad (desert) Hoard
Men, Buccaneers (water) Hoard

Level 1 to Level 5 treasure hoard in ascending value.

Dwarven Hoard
Dragon Hoard
Roc Hoard

The exact code or wording would be up to the author.

I have gotten done with AD&D yet but so far the additional treasure are added to give individuals treasures or to add to the hoard of high hit dice creatures.

[talysman]

Aug 9, 2012 7:45:02 GMT -6 robertsconley said:

The end results that for an OD&D clone that want to use treasure type the setup would be something like this.

Men, Normal (land) Hoard
Men, Dervish/Nomad (desert) Hoard
Men, Buccaneers (water) Hoard

Level 1 to Level 5 treasure hoard in ascending value.

Dwarven Hoard
Dragon Hoard
Roc Hoard

The exact code or wording would be up to the author.

I have gotten done with AD&D yet but so far the additional treasure are added to give individuals treasures or to add to the hoard of high hit dice creatures.

That's basically the approach I've been going for as I work on Liber Zero, except that I'm also trying various re-writes of the way probabilities were rolled.

Here's a really old example where I tried to use modifiers to a Target 20 roll:
9and30kingdoms.blogspot.com/2010/09/clone-project-treasure-table-ii.html

Here's a more recent example with a slightly different approach, which merges the two treasure tables (M&T and U&WA):
9and30kingdoms.blogspot.com/2011/06/liber-zero-treasure-tables.html

My current plan is something closer to the latter, but with some subtypes with names like those indicated in the first version (which just happen to start with the same letter as the closest LBB treasure type.) The subtypes will modify the rolls of the main type, and I'll toss in a few new subtypes of my own, like a "Merchant" subtype of the Adventurer's Trove (Type A).

[robertsconley]

So I looked at AD&D treasures including making a list of monsters categorized by treasure type. The big change is that many monsters have multiple treasure types. Including multiple instances of the same treasure type, for example Q (x10) meaning multiply the Q treasure type by ten.

Again the idea is not to figure out why Gygax assigned specific treasure types to individual monster but rather to understand the treasure types themselves.

List of monsters by Treasure Type
www.batintheattic.com/downloads/ADnD_Treasure_Types.doc

I kept the list in a word doc so you can edit it as you see fit.

A is no longer the Man Treasure Type, is not commonly used either being reserved for the Lich, Locathah, Men Bandits, Squid Giant, and Troglodytes

B to F are still pretty much like their OD&D counterpart with the same rough ascending order of value.

G is no longer just for dwarves. Elves are thrown in as well as a bunch of other creatures.

Interestingly the Roc has been removed from I but more creatures were assigned to this treasure type than OD&D. It also was used a lot with creatures with multiple treasure types, probably because of the Gem and Jewelry values.

H is still the hoard treasure for Dragons. Interesting the white dragons don't get this treasure type. Along with the Dragons the Archdevil Geryon and the Guardian Naga have this treasure type.

Now to the new types

J to N are meant to be assigned to individual monsters. When listed as part of a lair it looks to be incidental treasure. This especially clear for the various varieties of Giant Spiders.

O and P are low value coin treasure types, O is copper and silver, while P is silver and electrum

Q is a used a lot and in conjunction with other treasure types, It is the Gem treasure type.

R treasure type is similar to G but without any magic items.

S is the potion treasure type

T is the Scroll treasure type

U is a high value treasure type with Gems, Jewelry and magic items.

The elite monsters that get this are Orcus, Asmodeus, Tiamat the Chromatic Dragon, and interestingly enough Ixitxachitl Guards and Androsphinxs.

V is just magic items

W is similar to G and R but with map instead of magic items. It only used for the Men, Buccaneers.

X is miscellaneous magic items plus a potion, it been assigned to a lot of monster in conjunction with other treasure types.

Y is just gold pieces

Z is similar to H with a smaller number of magic items the monsters that get this are Men Dervishes, Men Nomads, and Will-o-the-wisp. Looks like there is a lot of wealth hidden underneath those camel sacks.

[cooper]

So the able treasure hunter will see right away that he is best served by going after pirates, buccaneers and mermen (type A3), and dwarves (type G) since these are only 1 HD monsters and have the richest hoards after dragons (type H). And dragons are a lot scarier

buccaneers, nomads, pirates, etc are best understood as super-heroes/lords+retainers without a fixed castle rather than a slew of 1hd men. Missing, interestingly from the monster section is the contents of a lord/wizard/ehp who actually have a fixed castle. Since they have as many retainers as buccaneers, nomads, and pirates one can assume they have a similar treasure type?

This applies to orcs, elves, and dwarves as well of course as their treasure is guarded not just by 1hd, but by heroes. It is no surprise to me that dwarves in 0d&d had the second best treasure type to dragons...there's a reason smaug usurped their homeland in the hobbit after all.

[paulg]

Not to derail from the larger question of what treasure types mean, but I've made an analysis of average treasure values that's somewhat at odds with values posted earlier.

A (Water) 80,600 gp
H 49,200 gp
A (Desert) 48,000 gp
A (Land) 40,450 gp
I 17,300 gp
F 10,000 gp
G 6,150 gp
D 5,200 gp
B 3,450 gp
C 2,450 gp
E 2,150 gp

I got these values from a Python script I wrote. The output looks like this:

ODnD Treasure Type Values: Minimum > 0 / Average / Maximum
----------------------------------------------------------
A (Land): 20 gp 40,357 gp 581,100 gp
A (Desert): 20 gp 48,134 gp 615,720 gp
A (Water): 120 gp 80,182 gp 663,440 gp
B: 10 gp 3,447 gp 500,110 gp
C: 10 gp 2,428 gp 52,180 gp
D: 10 gp 5,246 gp 102,300 gp
E: 10 gp 2,151 gp 60,200 gp
F: 20 gp 9,957 gp 155,660 gp
G: 160 gp 6,155 gp 505,040 gp
H: 10 gp 49,062 gp 559,820 gp
I: 20 gp 17,395 gp 555,500 gp
(Actual values from 100,000 rolls.)

It would be nice to get the relative average values of the treasure types established with some certainty.

[waysoftheearth]

I calculated the values I listed simply by multiplying the average amount of treasure that could occur, by the probability of that treasure occurring at all.

E.g., there is a 25% chance that treasure type A1 (A land) will contain 1,000-6,000 cp. Therefore (by my method) treasure type A1 contains an average of 875 cp.
Because 0.25 * (6000+1000)/2 = 875.

This would be repeated for copper, silver, gold, gems and jewellery, and the results summed for each treasure type.

If there's a better way to determine the average worth of a treasure type I'll be happy to adjust my figures accordingly.


edit: I suspect the above is pretty straight forward. What is less obvious is how to get the value of gems and jewellery, and I suspect that this may be where differences have appeared.

[geoffrey]

These are fascinating analyses!

[paulg]

If there's a better way to determine the average worth of a treasure type I'll be happy to adjust my figures accordingly.

edit: I suspect the above is pretty straight forward. What is less obvious is how to get the value of gems and jewellery, and I suspect that this may be where differences have appeared.

Gems are likely to be the biggest difference, but I found a couple of unrelated bugs in my script. I'll report back once I squash them.

[paulg]

After fixing a couple of bugs in my treasure type analysis script, my results look more like those supplied by waysoftheearth.

Even averaging several thousand runs, the high degree of randomness in treasure generation gives some differences in values from one run of the script to the next. For copper, the difference is one or two gold pieces. For gold, the difference is one or two hundred gold pieces either way. Still, the rankings of the treasure types relative to each other remains constant.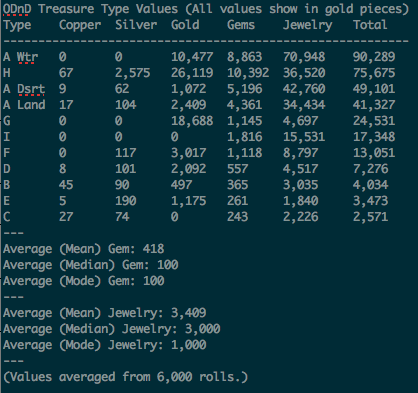



This is the chart waysoftheearth provided:



My copper values are about twice his, so he's probably using 1 gp = 100 cp, while I'm using 1 gp = 50 cp. Our silver and gold values are very close.

The remaining question is the gem and jewelry values. My values are much higher than wayoftheearth's, and change the treasure totals enough to change the relative rankings of treasure types.

(Gems are worth a mean of 55 gp each, while a piece of jewellery is worth an average of 1,137 gp).

My average values are 419 gp for gems and 3,410 gp for jewelry. My reading of gem and jewelry generation may be wrong. Let's take a closer look at that. Hopefully, one of you can set me straight.

Here's how I generate jewelry:

• roll d100
  
• if d100 <= 20, jewelry value is 3d6 times 100
  
• otherwise, if d100 <= 80, jewelry value is 1d6 times 1,000
  
• if d100 >= 81, jewelry value is 1d10 times 1,000
  

Doing this by hand a few times, I get: 3000, 4000, 6000, 1000, 2000, 7000, 4000, 6000, 9000, 4000. That's an average of 4,600 gp for each piece of jewelry, so reasonably close to my proposed average of 3,410 gp for only ten rolls.

The average chance for jewelry to be found in a treasure (averaged across all treasure types) is 35%. 35% of my average jewelry value is 1,193 gp. That's close to waysoftheearth's jewelry average of 1,137, but I don't know if that's how he calculated it.

Generation of gems is more complicated than generation of jewelry, with a far greater range of potential values. Here's how I read gem generation:

• roll d100
  
• 1-10 = 10 gp (but see below)
  
• 11-25 = 50 gp (but see below)
  
• 26-75 = 100 gp (but see below)
  
• 76-90 = 500 gp (but see below)
  
• 91-100 = 1,000 gp (but see below)
  

The value from the d100 roll isn't "fixed" until we make at least one d6 roll. If we roll a one on a d6, the gem gets bumped to the next highest value (e.g.--a 50 gp gem becomes a 100 gp gem).

Additionally, (and this may be the part I'm misreading) once a gem gets bumped to it's new value, that value still isn't fixed. We roll d6 again. A roll of one means the gem gets bumped to the next higher value (e.g.--our 100 gp gem increases again to a 500 gp gem).

Value bumping continues for the gem until we roll a d6 result other than one. At that point, the value of the gem is final. If your string of one's takes you past the 1,000 gp mark, use these tiers: 5,000; 10,000; 25,000; 50,000; 100,000; and 500,000 gp.

I'll roll a few gems by hand: 1000, 500, 500, 100, 100, 10, 100, 100, 10, and 100 gp. That's an average (mean) of 242 gp--less than the 419 gp average I propose, and more than the 55 gp average waysoftheearth provides.

With a mode of 100, and values that only get bumped up, we're unlikely to get a mean of less than 100 gp. Possibly, as I surmise for jewelry, wayoftheearth's gem value of 55 gp averages gems that exist with those that do not.

[waysoftheearth]

You are spot on Paulg! Thanks for making me double check -- I found an error in my mean gem and jewellery calculations. With this corrected, my revised figures are very close to yours.

(The funny thing is, I had it right originally but though to myself "those figures are WAY too high", and by thinking to fix it I actually broke it).


Gems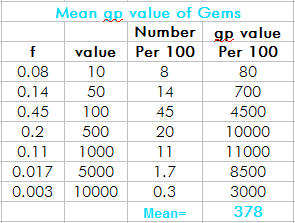

I ignored gems that are extremely unlikely to occur. Being so rare, they don't make much difference to the average in any case.


Jewellery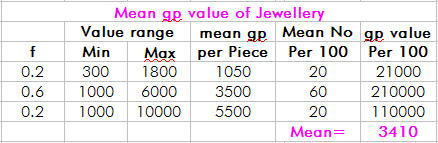



Of course this correction further exaggerates the importance of gems (and especially jewellery) in the treasure tables. Everything else (except magic items) is worth peanuts by comparison.

Updated sorted mean treasur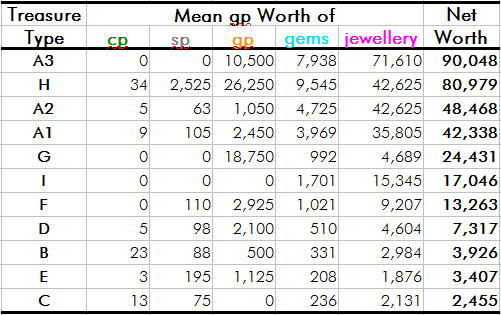e values


Updated percentage values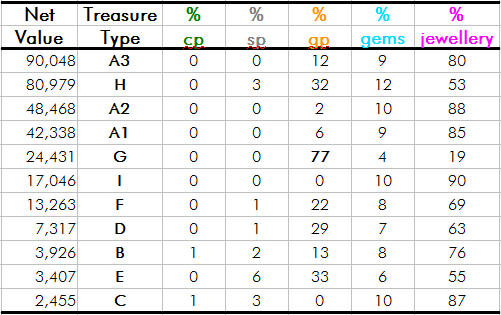



The value "order" of types B, C, D, E, F is revised to:

C > E > B > D > F

So Type C (ogres, gargoyles, lycanthropes, minotaurs, gnomes) is the least valuable treasure type in the game, and Type D (probably the most frequently encountered type in the early game -- orcs, hobgoblins, gnolls, trolls, etc.) is almost four times as valuable.

Thanks for your diligence Paulg, have an exalt!

[aldarron]

Awsome work gentlemen! Definetly takes out the guesswork. For your analyzing pleasure, if it strikes your fancy, here is the Treasure Table given in Beyond This Point be Dragons:



The table (originally on the bottom and top of two seperate pages), is either an older version of the one in the 3lbb's or Arneson's revision of an older table. Most likely the latter, since it is somewhat differently organized and the footnote info in the 3lbb's is incorporated in the text.

There are lots of small differences and there is also no type I. There's also some difference in generating gems and jewelry:

Gems: roll a d6. 1 = 1000; 2 = 500; 3-6 = 100
Roll another d6 for each gem. Results of 1 bump up to next highest value. Values above 1000 are 5000, 10,000, 20,000 and 5000.

Jewelry: Roll d6. 1-3 = 100; 4-6 = 1000.
For base 100, roll 3d6 and multiply by 100
For base 1000, roll 1d6 and multiply by 1000.

It's worth noting too that the following monsters have Lair treasure types that differ from the 3lbb's (3lbb in parenthesis):


Orcs - Type A (D)

Ogres - Type B (C)

Wraiths - Type D (E)

Vampires - Type E (F)

Wyvern - Type E (F)

Dragons - Type D (H)

Lycanthropes - Type B (C)

[aldarron]

Okay, I used the method employed by WotE, on the BTPbD tables. Here's what I got:

Gems average value: 386 GP each.

Jewelry average value: 2275 GP each.

Type average values (greatest to least):

A:water – 70,114
H – 59,451
A:land – 28,466
A:Desert – 14,059
F – 4901
D – 4496
E – 2388
G – 2163
C – 1107
B - 363

Observations: There's some really significant revisions here. More than I expected. Gems are about the same in value to 3lbb's but jewelry is significantly less. The value order is also changed in significant ways. In particular Type B (ghouls, wights, ogres, hydras, lycanthropes, Nixies) is now the least. Type A:land is here almost twice as valuable as Type A:desert, whereas in the 3lbb table, desert is more valuable than land by about 20%. Type G (Rocs) is also a lot less due to the reduction in Jewelry value. In fact all the treasure types are significantly less than the OD&D amounts.

[aher]

I wanted to develop an exact result for the mean value of a gem, based on theory, one that kept the rare gems valued from 5,000 gp to 500,000 gp, without resorting to simulations.

The theoretical result I got (417.563 gp) matches the result paulg got (418 gp) by simulation.

Aug 11, 2012 20:28:51 GMT -6 waysoftheearth said:

I ignored gems that are extremely unlikely to occur. Being so rare, they don't make much difference to the average in any case.

WotE is right that the probability of getting a gem greater than 1,000 gp is tiny -- 2.32767%. The probability of getting a 500,000 gp gem is a mere 3 in a million. But these "black swans" do skew the mean. The distribution has a skewness of 120.86 and a kurtosis of 36,821.2, compared to a normal distribution which has skewness 0 and kurtosis 3.

To put these rare gems back into the theoretical account of the distribution, I took the following steps:

In Mathematica, I created a categorical distribution that captures the essence of rolling a d100 and using the table on page 40 of volume 2 in order to get an initial value for the gem. However, instead of assigning the gem a value in gp, I merely assign it a category, 1 through 5. Call this distribution X:

gemtable = EmpiricalDistribution[{.1, .15, .5, .15, .1} -> {1, 2, 3, 4, 5}]

Next I create a distribution that counts how many 1s I roll on a d6 before I get some other result. In probability theory, this is known as a geometric distribution:

d6while1 = GeometricDistribution[5/6]

Then I lumped all the probability mass in this distribution to the left of 11 together. Call this distribution Y:

pdfd6while1max11[x_] =
Which[x < 0, 0, x >= 0 && x <= 10, PDF[d6while1, x], x == 11,
 Sum[PDF[d6while1, k], {k, 11, \[Infinity]}], x > 11, 0]

Now we want the distribution Z=X+Y. We do this by "convolving" the probability mass functions of the two distributions whose random variables you're adding. Here is the code to perform the convolution:

gempdf[k_] := Sum[PDF[gemtable,j] pdfd6while1max11[k-j], {j, 0, 11}]

Again we want a "censored distribution" that lumps everything to the left of 10 together, since there are only 11 categories of gems:

gempdflist = Append[gempdf[#]&/@Range[1,10], Fold[Plus,0,gempdf[#]&/@Range[11,16]]]

Here is the "lookup table" that maps gem categories into gold piecess:

gp = {10, 50, 100, 500, 1000, 5000, 10000, 25000, 50000, 100000, 500000}

Finally, here is the probability distribution we are after:

gems = EmpiricalDistribution[gempdflist -> gp]

Now we can operate on this distribution like any other built-in distribution, in order to find its statistics:

Mean[gems]
417.563

Median[gems]
100

StandardDeviation[gems]
1504.61

Skewness[gems]
120.86

Kurtosis[gems]
36821.2

Probability[x > 1000, x \[Distributed] gems]
0.0232767

(* Generate 100 random gems *)
RandomVariate[gems,100]
{1000,10,100,100,100,100,1000,100,1000,100,100,100,10,1000,1000,500,100,100,500,100,50,100,50,100,100,1000,100,100,50,1000,100,1000,500,100,500,500,500,500,10,500,100,100,100,1000,100,100,100,100,100,100,100,1000,100,1000,100,100,500,100,5000,10,500,100,1000,100,500,500,50,500,100,100,100,100,10,1000,500,50,500,10,500,50,100,10000,50,100,100,500,1000,1000,100,500,100,500,100,50,500,500,100,100,100,100}

(* Count how many of these 100 random gems > 1000 gp. We expect about 2. *)
Select[%,#>1000&]
{5000,10000}

(* Chance of a half-million gp gem is one in how many *)
1/gempdflist[[11]]
334067.

(* Create a table with all the probability values *)
TableForm[Table[{x,PDF[gems,x]},{x,gp}],TableHeadings->{None,{"gp","Probability"}}]


And here is the table of probabilities produced by that last line of code:

gp	Probability
10	0.0833333
50	0.138889
100	0.439815
500	0.198302
1000	0.116384
5000	0.0193973
10000	0.00323288
25000	0.000538814
50000	0.0000898023
100000	0.000014967
500000	2.99341*10^-6

The probabilities from 10 gp to 1,000 gp don't differ all that much from WotE, but those big gems with tiny probabilities on the long tail do skew the results by a noticeable amount. The difference between WotE's mean (378 gp) and mine (417.563 gp) is about 40 gp.

Since I never trust my own calculations, I always try to reproduce the results in some other way. So I did write a monte carlo simulation in Lisp called gems.lsp, and you can see it here in my pastebin. If you have a Lisp interpreter and want to try it yourself, you can use a command-line like so:

elisha@ubuntu:~/workspace$ clisp gems.lsp 10000000
Number of runs 10000000
Total value of gems (in gp) 4174236350
Mean value of gems 417.4236
Standard deviation 1486.8490

As you can see, I ran this simulation 10,000,000 times (it didn't take that long), because 500,000 gp gems are so rare, and the resulting mean (417.4236 gp) is a good match for the exact result I got in Mathematica (417.563 gp).